About Linear Actuators
An Authoritative List of the Best Linear Actuator Manufacturers Available
Linear actuators are devices that are utilized by an array of industries to convert nonlinear energy into linear motion. They are powered by a wide variety of energy sources including pneumatic, mechanical, hydraulic, electro-mechanical and piezoelectric. Each source of energy has its own particular conversion mechanism. The main goal of these devices is basically to convert small nonlinear energy into linear motion of increased magnitude to be used for a particular process, machine or application. Examples of applications range from giant hydraulic rams to DVD tray openers. Different designs allow actuators to work in almost any kind of environment including underwater, corrosive, cryogenic, radiation and vacuum environments. Different types of actuators are classified considering four main factors; size, output, potential and power requirements.
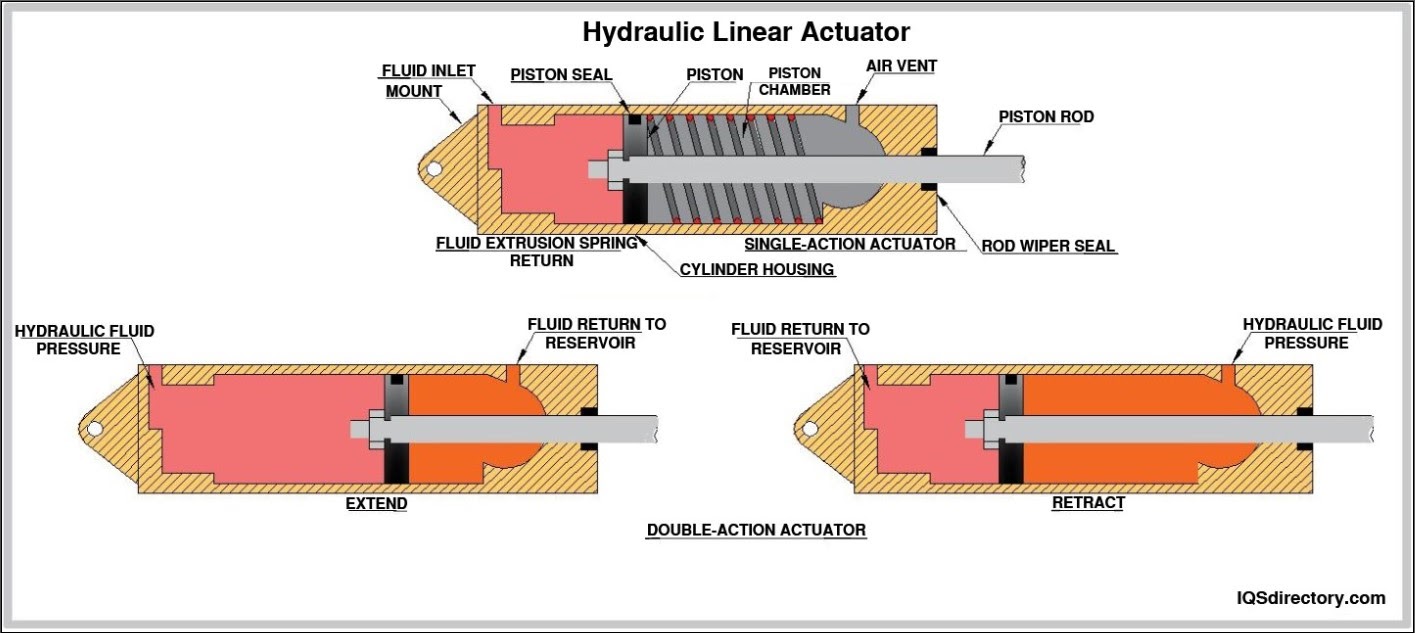
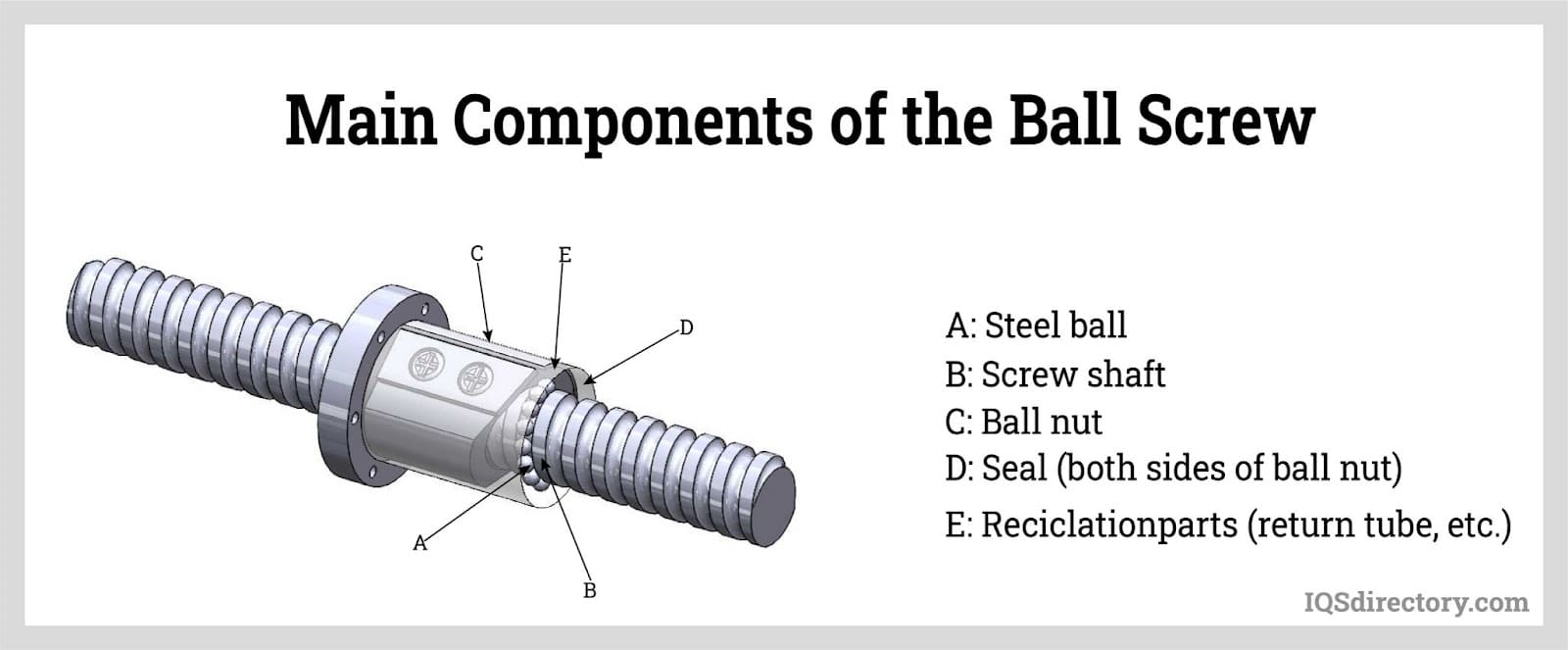
The most utilized method of classification for linear actuators involves the method used to convert energy into mechanical linear energy. For example, a DC actuator converts DC electrical energy to provide mechanical linear motion, whereas 12 volt linear actuators follow the same process, but with 12 volts of energy. On the other hand, ball screw actuators convert rotary motion into mechanical energy to produce mechanical linear motion. This is done through a combination of ball screws and ball nuts. Hydraulic actuators utilize some sort of hydraulic fluid and pneumatic actuators position control valves using linear motion by converting various forms of energy, normally air pressure, into mechanical energy.
Other types of linear actuators include valve actuators, which supply linear movement to valves by using an assortment of screw assemblies. Servo actuators maintain the proper functions of another mechanism or equipment part by providing position control, utilizing linear motion. Miniature linear actuators are used in small spaces that require large payloads and electric actuators convert electricity into mechanical energy. An example of compact, simple and efficient devices is rotary actuators. These devices rotate an output shaft through a fixed arc to produce oscillating power. It can produce high instant torque in either direction, requires limited space and simple mountings. Basic linear actuators, also known as electromechanical actuators, use electrical power to achieve mechanical force through linear actuators. Despite the many different types of linear actuators and the energy sources used to power them, they all pursue the same objective, to create linear motion by convert some form of energy.





 Air Cylinders
Air Cylinders Assembly Machinery
Assembly Machinery Ball Bearings
Ball Bearings Electric Motors
Electric Motors Fractional Horsepower Motors
Fractional Horsepower Motors Friction Materials
Friction Materials Linear Actuators
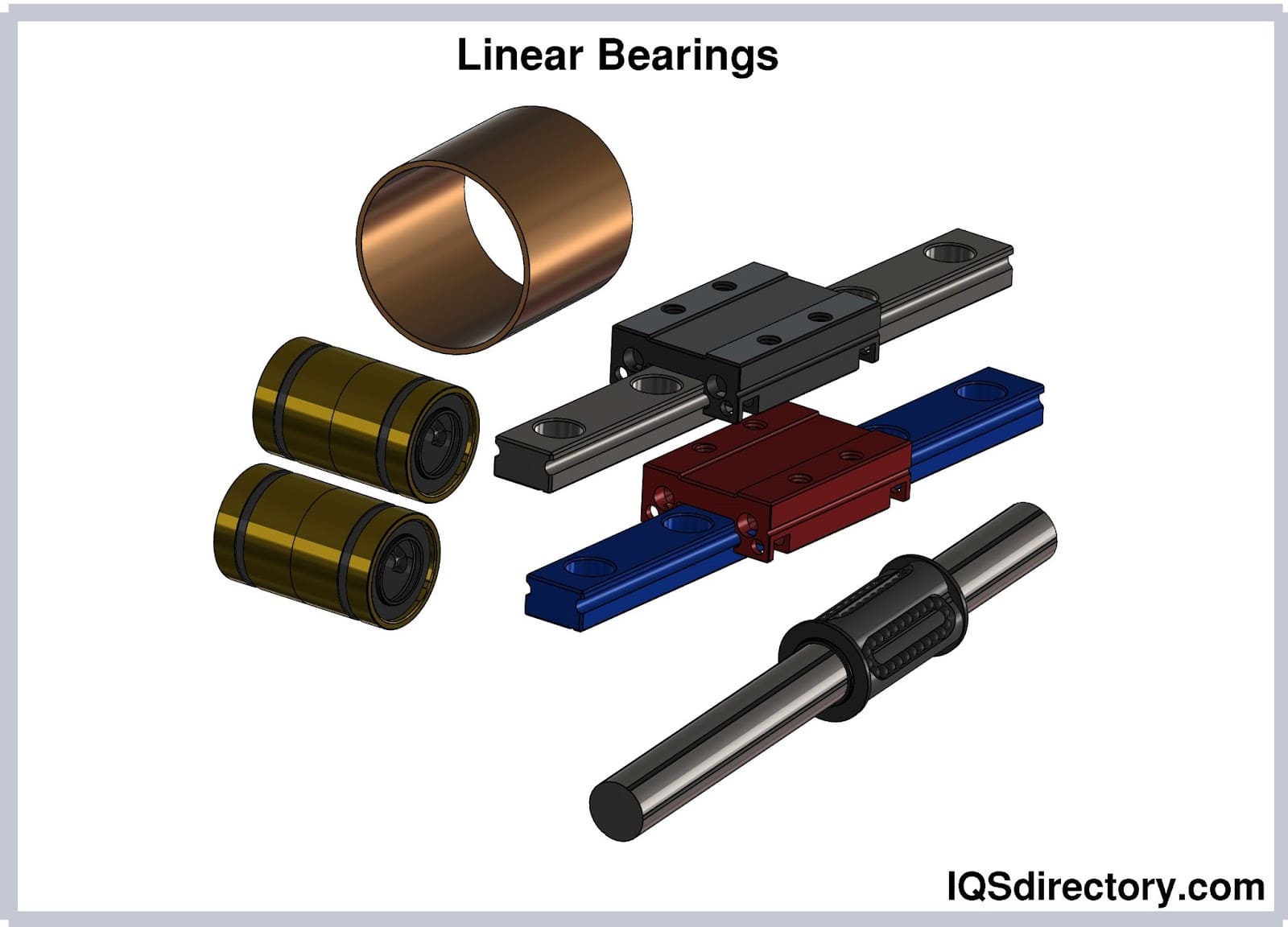
Linear Actuators Linear Bearings
Linear Bearings Linear Slides
Linear Slides Castings & Forgings
Castings & Forgings Bulk Material Handling
Bulk Material Handling Electrical & Electronic Components
Electrical & Electronic Components Flow Instrumentation
Flow Instrumentation Hardware
Hardware Material Handling Equipment
Material Handling Equipment Metal Cutting Services
Metal Cutting Services Metal Forming Services
Metal Forming Services Metal Suppliers
Metal Suppliers Motion Control Products
Motion Control Products Plant & Facility Equipment
Plant & Facility Equipment Plant & Facility Supplies
Plant & Facility Supplies Plastic Molding Processes
Plastic Molding Processes Pumps & Valves
Pumps & Valves Recycling Equipment
Recycling Equipment Rubber Products & Services
Rubber Products & Services